How to Draw Phase Plane Using Eigenvectors
Phase Portraits of Linear Systems
Consider a In this section we study the qualitative features of the phase portraits, obtaining a classification of the different possibilities that can arise. 1 reason that this is important is considering, as nosotros volition see presently, it will be very useful in the study of nonlinear systems. The classification will not exist quite consummate, considering nosotros'll leave out the cases where 0 is an eigenvalue of ![]() .
.
The commencement step in the classification is to find the characteristic polynomial, ![]() , which volition exist a quadratic: we write it as
, which volition exist a quadratic: we write it as ![]() where
where ![]() and
and ![]() are existent numbers (assuming every bit usual that our matrix
are existent numbers (assuming every bit usual that our matrix ![]() has real entries). The nomenclature will depend mainly on
has real entries). The nomenclature will depend mainly on ![]() and
and ![]() , and we brand a nautical chart of the possibilities in the
, and we brand a nautical chart of the possibilities in the ![]() plane.
plane.
At present nosotros look at the discriminant of this quadratic, ![]() . The sign of this determines what type of eigenvalues our matrix has:
. The sign of this determines what type of eigenvalues our matrix has:
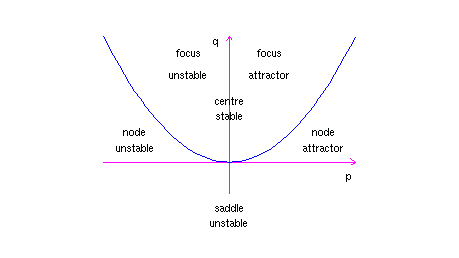
Each of these cases has subcases, depending on the signs (or in the complex case, the sign of the real part) of the eigenvalues. Notation that ![]() is the product of the eigenvalues (since
is the product of the eigenvalues (since ![]() ), and so for
), and so for ![]() the sign of
the sign of ![]() determines whether the eigenvalues have the same sign or opposite sign. We will ignore the possibility of
determines whether the eigenvalues have the same sign or opposite sign. We will ignore the possibility of ![]() , every bit that would hateful 0 is an eigenvalue.
, every bit that would hateful 0 is an eigenvalue.
The sum of the eigenvalues is ![]() , and then if they accept the same sign this is opposite to the sign of
, and then if they accept the same sign this is opposite to the sign of ![]() . If the eigenvalues are complex, their real part is
. If the eigenvalues are complex, their real part is ![]() .
.
Another important tool for sketching the phase portrait is the following: an eigenvector ![]() for a real eigenvalue
for a real eigenvalue ![]() corresponds to a solution
corresponds to a solution ![]() that is always on the ray from the origin in the direction of the eigenvector
that is always on the ray from the origin in the direction of the eigenvector ![]() . The solution
. The solution ![]() is on the ray in the reverse direction. If
is on the ray in the reverse direction. If ![]() the move is outward, while if
the move is outward, while if ![]() it is inward. Equally
it is inward. Equally ![]() (if
(if ![]() ) or
) or ![]() (if
(if ![]() ), these trajectories approach the origin, while as
), these trajectories approach the origin, while as ![]() (if
(if ![]() ) or
) or ![]() (if
(if ![]() ) they go off to
) they go off to ![]() . For circuitous eigenvalues, on the other hand, the eigenvector is not so useful.
. For circuitous eigenvalues, on the other hand, the eigenvector is not so useful.
In addition to a nomenclature on the basis of what the curves expect like, we will want to discuss the stability of the origin every bit an equilibrium point.
Here, then, is the classification of the phase portraits of ![]() linear systems.
linear systems.
- If
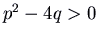 ,
, 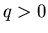 and
and 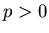 , we accept 2 negative eigenvalues. There are directly-line trajectories corresponding to the eigenvectors. The other trajectories are curves, which come up in to the origin tangent to the ``slow'' eigenvector (corresponding to the eigenvalue that is closer to 0), and as they go off to
, we accept 2 negative eigenvalues. There are directly-line trajectories corresponding to the eigenvectors. The other trajectories are curves, which come up in to the origin tangent to the ``slow'' eigenvector (corresponding to the eigenvalue that is closer to 0), and as they go off to 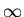 approach the direction of the ``fast'' eigenvector.
approach the direction of the ``fast'' eigenvector. This case is called a node. It is an attractor.
Here is the motion-picture show for the matrix
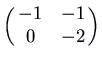 , which has characteristic polynomial
, which has characteristic polynomial 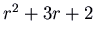 . The eigenvalues are
. The eigenvalues are 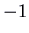 (tedious) and
(tedious) and 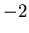 (fast), respective to eigenvectors
(fast), respective to eigenvectors 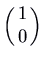 and
and 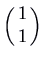 respectively.
respectively. 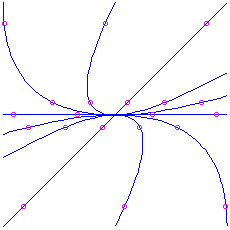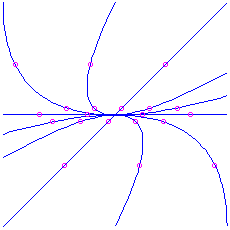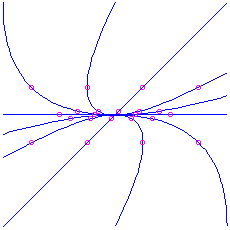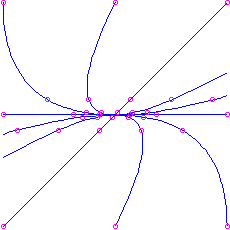
- If
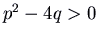 ,
, 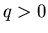 and
and  , we have two positive eigenvalues. The motion-picture show is the same as in the previous case, except with the arrows reversed (going outward instead of inward). Again the curved trajectories come in to the origin tangent to the ``slow'' eigenvector (corresponding to the eigenvalue that is closer to 0), and as they go off to
, we have two positive eigenvalues. The motion-picture show is the same as in the previous case, except with the arrows reversed (going outward instead of inward). Again the curved trajectories come in to the origin tangent to the ``slow'' eigenvector (corresponding to the eigenvalue that is closer to 0), and as they go off to  arroyo the direction of the ``fast'' eigenvector. This is also a node, but information technology is unstable. Hither is the picture for the matrix
arroyo the direction of the ``fast'' eigenvector. This is also a node, but information technology is unstable. Hither is the picture for the matrix 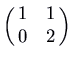 , which has characteristic polynomial
, which has characteristic polynomial 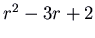 . The eigenvalues are
. The eigenvalues are 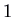 (irksome) and
(irksome) and 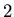 (fast), corresponding to eigenvectors
(fast), corresponding to eigenvectors 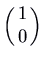 and
and 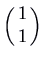 respectively. Notation that the picture is exactly the same as what we had for the attractor node, except that the direction of time is reversed (the animation is run backwards).
respectively. Notation that the picture is exactly the same as what we had for the attractor node, except that the direction of time is reversed (the animation is run backwards). 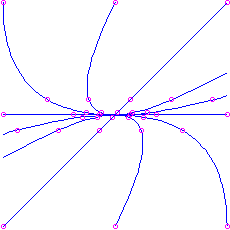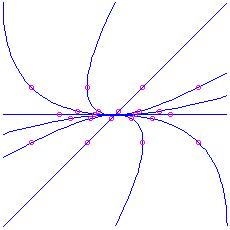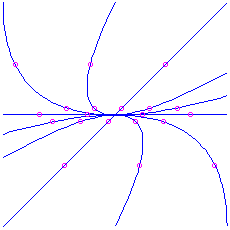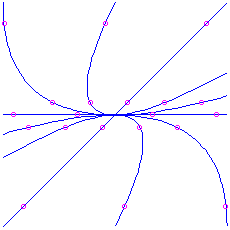
- If
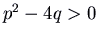 and
and 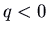 , we have one positive and one negative eigenvalue. Again there are straight-line trajectories respective to the eigenvectors, with the motion outwards for the positive eigenvalue and inward for the negative eigenvalue. These are the but trajectories that approach the origin (in the limit every bit
, we have one positive and one negative eigenvalue. Again there are straight-line trajectories respective to the eigenvectors, with the motion outwards for the positive eigenvalue and inward for the negative eigenvalue. These are the but trajectories that approach the origin (in the limit every bit 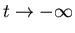 for the positive and
for the positive and 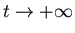 for the negative eigenvalue). The other trajectories are curves that come in from
for the negative eigenvalue). The other trajectories are curves that come in from 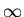 asymptotic to a straight-line trajectory for the negative eigenvalue, and go back out to
asymptotic to a straight-line trajectory for the negative eigenvalue, and go back out to 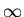 asymptotic to a directly-line trajectory for the positive eigenvalue.
asymptotic to a directly-line trajectory for the positive eigenvalue. This is called a saddle. It is unstable. Annotation that if you outset on the straight line in the direction of the negative eigenvalue you do approach the equilibrium bespeak as
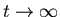 , but if you lot starting time off this line (fifty-fifty very slightly) you finish up going off to
, but if you lot starting time off this line (fifty-fifty very slightly) you finish up going off to 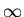 .
. Here is the picture for the matrix
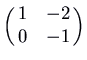 , which has characteristic polynomial
, which has characteristic polynomial 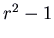 . The eigenvalues are
. The eigenvalues are 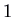 and
and 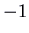 , corresponding to eigenvectors
, corresponding to eigenvectors 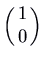 and
and 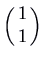 respectively.
respectively. 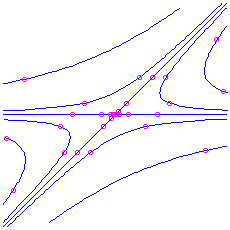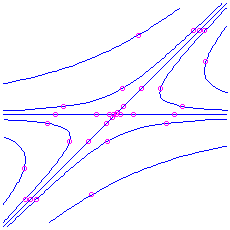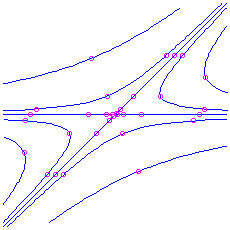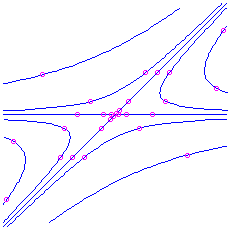
- If
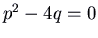 , we accept only one eigenvalue
, we accept only one eigenvalue 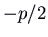 (a double eigenvalue). There are two cases here, depending on whether or non at that place are ii linearly independent eigenvectors for this eigenvalue.
(a double eigenvalue). There are two cases here, depending on whether or non at that place are ii linearly independent eigenvectors for this eigenvalue. - If there are ii linearly independent eigenvectors, every nonzero vector is an eigenvector. Therefore we have direct-line trajectories in all directions. The move is e'er inward if the eigenvalue is negative (which ways
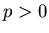 ), or outwards if the eigenvalue is positive (
), or outwards if the eigenvalue is positive (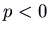 ). This is called a atypical node. Information technology is an attractor if
). This is called a atypical node. Information technology is an attractor if 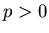 and unstable if
and unstable if 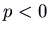 .
. Here is the moving picture for the matrix
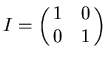 , which has feature polynomial
, which has feature polynomial 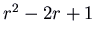 and eigenvalue
and eigenvalue 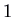 . It is unstable. For the matrix
. It is unstable. For the matrix 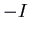 we would have an attractor: the aforementioned picture except with time reversed.
we would have an attractor: the aforementioned picture except with time reversed. 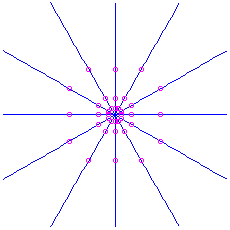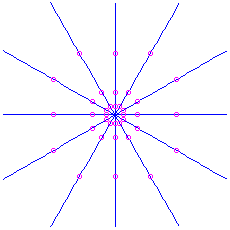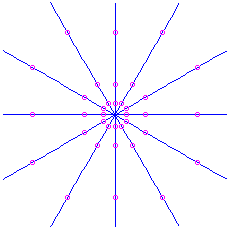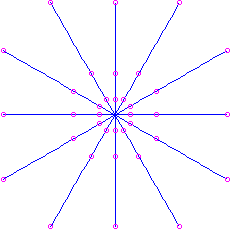
- If there is only 1 linearly contained eigenvector, in that location is merely i directly line. The other trajectories are curves, which come up in to the origin tangent to the directly line trajectory and curve around to the opposite direction. Trajectories on opposite sides of the straight line class an ``S'' shape. The way to tell whether it is a forwards S or backwards South is to wait at the direction of the velocity vector
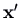 at some point off the straight line.
at some point off the straight line. This is called a degenerate node. Again, it is an attractor if
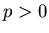 and unstable if
and unstable if 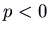 .
. Hither is the picture for the matrix
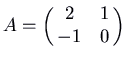 , which has characteristic polynomial
, which has characteristic polynomial 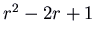 , eigenvalue 1 and eigenvector
, eigenvalue 1 and eigenvector 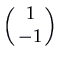 . It is unstable. Note that the trajectories in a higher place the straight line
. It is unstable. Note that the trajectories in a higher place the straight line 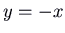 are come out of the origin heading to the left along that line, and those below the line come out heading to the right. Thus the S is forwards. To check this, you could calculate the velocity vector at, for instance,
are come out of the origin heading to the left along that line, and those below the line come out heading to the right. Thus the S is forwards. To check this, you could calculate the velocity vector at, for instance, 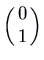 , which is
, which is 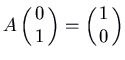 . Since that points to the correct, it's piece of cake to run across the S must be forwards.
. Since that points to the correct, it's piece of cake to run across the S must be forwards. 
- If there are ii linearly independent eigenvectors, every nonzero vector is an eigenvector. Therefore we have direct-line trajectories in all directions. The move is e'er inward if the eigenvalue is negative (which ways
- If
 and
and 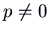 , we have complex eigenvalues
, we have complex eigenvalues 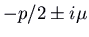 . The solutions are of the form
. The solutions are of the form 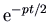 times some combinations of
times some combinations of 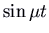 and
and 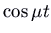 . The picture is a screw, also known every bit a focus. Information technology is an attractor if
. The picture is a screw, also known every bit a focus. Information technology is an attractor if 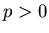 , every bit the factor
, every bit the factor 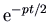 makes all solutions approach the origin as
makes all solutions approach the origin as 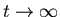 , and unstable if
, and unstable if 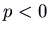 , as in that instance the gene
, as in that instance the gene 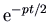 makes all solutions (except the one starting at the equilibrium signal itself) go off to
makes all solutions (except the one starting at the equilibrium signal itself) go off to 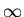 as
as 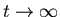 . Nosotros can calculate a velocity vector to check if the motion is clockwise or counterclockwise.
. Nosotros can calculate a velocity vector to check if the motion is clockwise or counterclockwise. Here is the picture show for the matrix
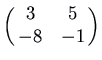 , which has feature polynomial
, which has feature polynomial 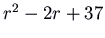 and eigenvalues
and eigenvalues 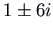 . It is unstable. To check that the motion is clockwise, yous could notation that the velocity vector at
. It is unstable. To check that the motion is clockwise, yous could notation that the velocity vector at 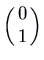 is
is 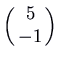 , which is to the right.
, which is to the right. 
- Finally, if
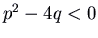 and
and 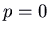 , we have pure imaginary eigenvalues
, we have pure imaginary eigenvalues 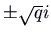 . The solutions involve combinations of
. The solutions involve combinations of 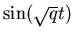 and
and 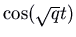 . These are all periodic, with menstruum
. These are all periodic, with menstruum 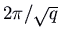 . The trajectories plow out to be ellipses centred at the origin. The pic is known every bit a eye. Since a solution that starts nigh the origin just goes around and around the same ellipse, never getting any closer to or farther from the equilibrium than the closest and farthest points on the ellipse, this equilibrium is stable but non an attractor. Once again nosotros can calculate a velocity vector to see whether the movement is clockwise or counterclockwise.
. The trajectories plow out to be ellipses centred at the origin. The pic is known every bit a eye. Since a solution that starts nigh the origin just goes around and around the same ellipse, never getting any closer to or farther from the equilibrium than the closest and farthest points on the ellipse, this equilibrium is stable but non an attractor. Once again nosotros can calculate a velocity vector to see whether the movement is clockwise or counterclockwise. Here is the moving picture for the matrix
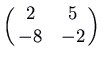 , which has feature polynomial
, which has feature polynomial 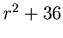 and eigenvalues
and eigenvalues 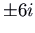 . Again you tin can bank check that the motion is clockwise by noting that the velocity vector at
. Again you tin can bank check that the motion is clockwise by noting that the velocity vector at 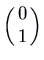 is
is 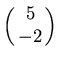 , which is to the right.
, which is to the right. 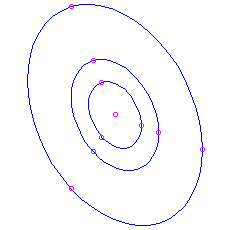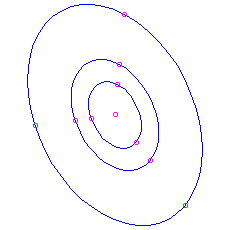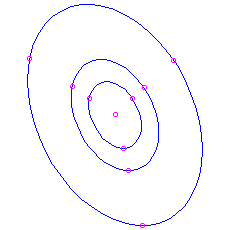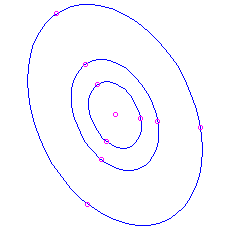
- Near this certificate ...
Robert Israel
2002-03-24
Source: https://www.math.ubc.ca/~israel/m215/linphase/linphase.html
0 Response to "How to Draw Phase Plane Using Eigenvectors"
Postar um comentário